Assignment 9:

Pedal Triangles

by
Jenny Johnson

Constructing a Pedal Triangle

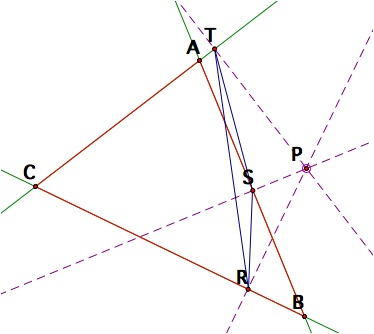
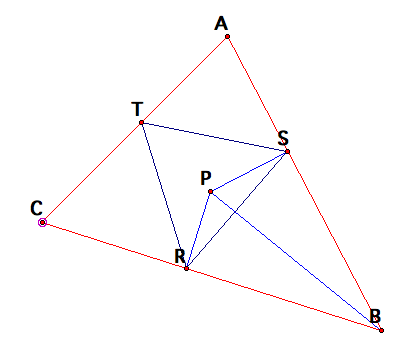
First, we are going to construct a triangle with vertices A, B, and C. Then we make an arbitrary point P and construct a perpendicular line from P to each line containing sides AB, BC, and AC. Since the point P could be outside the triangle, the perpendicular lines might also be found outside the triangle. That is why we construct the perpendicular to the lines containing the sides instead of the sides themselves. The three points at which the perpendiculars intersect the lines containing the triangles’ sides (labeled R, S, T) can be formed into a triangle. This triangle is called the Pedal Triangle. In the picture below, the red segments are the sides of the triangle, the green lines are the lines containing the sides, the purple dashed lines are the perpendiculars constructed from point P, and the blue triangle is the pedal triangle.

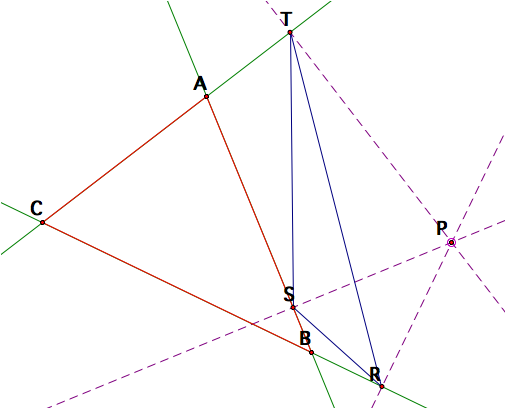
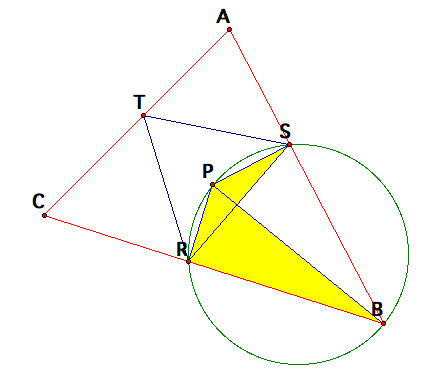
If we move the point P outside triangle ABC, the pedal triangle is altered, as shown in the pictures below.

For your explorations with the pedal triangle, click here. This GSP file contains a pedal triangle script tool.

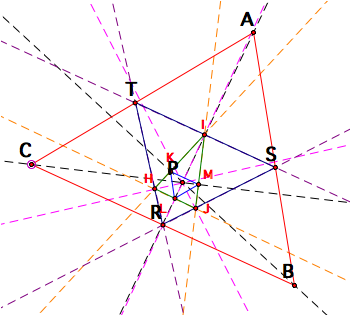
Now, we construct the pedal triangle of the pedal triangle and call it triangle HIJ. Then we find the pedal triangle of triangle HIJ, which is triangle KLM. These constructions can be seen in the picture below.

Without the construction lines, we get the following picture.

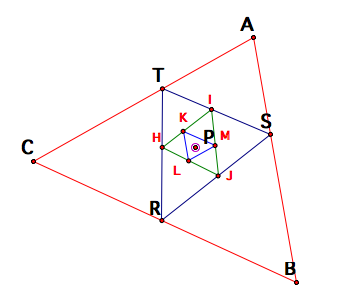
How is triangle KLM related to the original triangle ABC?

First, I measured each of angles of the original triangle ABC and each of the angles of triangle KLM on Geometer’s Sketchpad. I then moved point P and the vertices A, B, and C and found that angle A was always congruent to angle KLM, angle B was always congruent to angle MKL and angle C was always congruent to angle KML. This, of course, is not a proof that the triangles are similar, but it helps me see that I can find a way to prove the triangles are similar.

Can we prove that DKLM is similar to DABC?

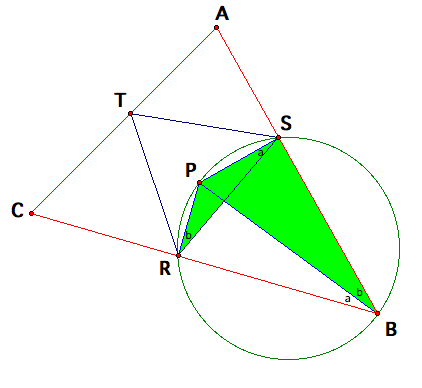
Let’s first look at the original triangle ABC with point P and the pedal triangle RST. We see that the quadrilateral PSBR has two right angles at vertex S and vertex R.

This creates two right triangles PSB and PRB. Based on what we know about circles, we can make a few conjectures. There is a theorem called the inscribed angles theorem that states that any angle θ inscribed in a circle is half the measure of the central angle 2θ and the intercepted arc 2θ. A corollary of this theorem is that a right inscribed angle intercepts the circle at the endpoints of the diameter. The angle measure does not change as its vertex is moved to different positions on the circle. In our picture, this would mean that we can form a circle with PB as the diameter and point S would lie on the circle. Similarly, R would have to lie on the same circle with diameter PB. We thus can draw the circle with diameter PB.

Using the inscribed angle theorem again, we see that angle PSR and angle PBR both intercept the same arc PR.

This means angle PSR and angle PBR are both half the measure of arc PR and therefore equal to each other. Let’s say the measure of these two angles is a.

Similarly, if we look at angles PRS and PBS, then we see that they both intercept arc PS. Thus, they are also equal angles and we’ll label them with the letter b.

Looking at quadrilaterals PTCR and PTAS, we see the same relationship with inscribed angles. Thus, we can label all the angles that are equal as follows.

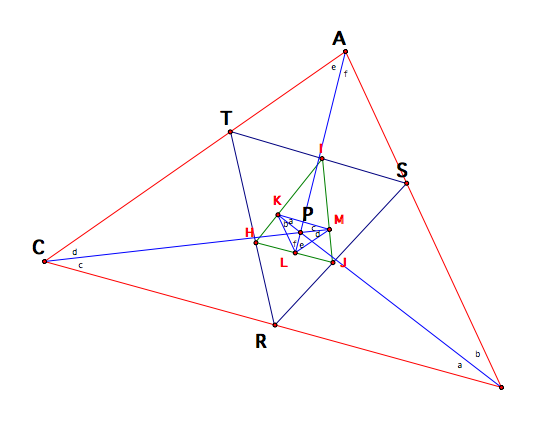
Now let’s zoom in on the pedal triangle TSR and its pedal triangle HIJ.

Using the same reasoning as above, angle PHR and angle PJR both intercept a circle at the endpoints of its diameter PR. Thus, we can form a circle with diameter PR and we can expect H and J to both lie on that circle.

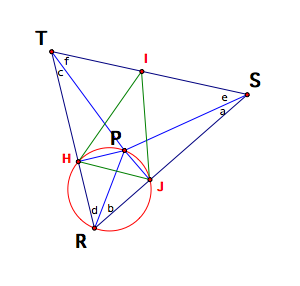
Now we can see that angles HRP and HJP intercept the same arc HP, so the measures of their angles are equal. Since the measure of angle HRP is d, we know angle HJP must be d as well.

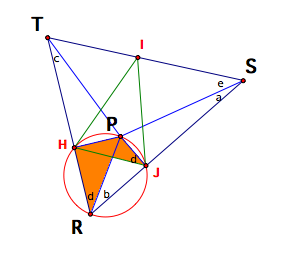
Angles PRJ and PHJ are also equal because they intercept the same arc PJ and both are equal to the measure of b.

Looking at quadrilaterals PITH and PISJ, we see the same relationship with inscribed angles. Thus, we can label all the angles that are equal as follows.

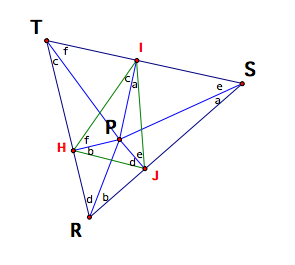
Now let’s zoom in on the pedal triangle HIJ and its pedal triangle KLM.

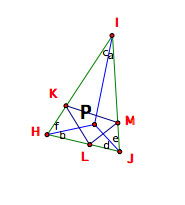
Using the same reasoning as above again, angle PLJ and angle PMJ both intercept a circle at the endpoints of its diameter PJ. Thus, we can form a circle with diameter PJ and we can expect L and M to both lie on that circle. Also, angles LJP and LMP intercept arc PL and therefore will both equal d, and angles PLM and PJM intercept arc PM and will equal e.

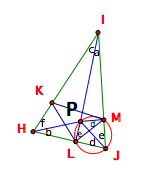
Applying the intercepted arc theorem to the entire triangles, we find that the angle measures of both triangles are as follows.

So are the triangles KLM and ABC similar triangles?

Let’s look at the angle measures of the two triangles.

We see that angle B has a measure of a + b. Angle MKL in the pedal triangle of the pedal triangle of the pedal triangle is also a + b. Thus, angle B = angle MKL. Angle C has a measure of d + c. Angle KML also has a measure of c + d. Thus, angle C = angle KML. Angle A has a measure of e + f. Angle KLM also has a measure of e + f. Thus, angle A = angle KLM. Since the three angles in triangle KLM are congruent to the three angles in triangle ABC, we know that they are similar triangles.

Return